【裸板驱动】常见滤波函数分享

一、源码

mod_filter.c源码

/*
文件功能：
	提供不同的滤波函数
用法介绍：
	1.定义相关滤波函数的结构体
	2.使用对应函数进行数据处理
作者：
	春风催雪
更新记录：
	2022-1-17>>V0.1：初次整理
*/
#include "include.h"

/*
	描述：对数据进行均值滤波
	pAverage：均值滤波相关数据结构体指针，详细参考AVERAGEPARAM
	Input：实际输入值
	返回：滤波后的输出值
	注意：均值滤波长度要在200以内，且需要考虑数据总和不能超过int32_t
*/
int32_t Mod_Filter_Average(AVERAGEPARAM *pAverage, int32_t Input)
{
	uint8_t i;
	
	if((pAverage->Length < 1) || (pAverage->Length > 200))  //超长退出
	{
		return 0;
	}
	
	if(pAverage->OnceTF == 0)  //初次进入
	{
		pAverage->OnceTF = 1;
		pAverage->DatPos = 0;
		for(i=0; i<pAverage->Length; i++)
		{
			pAverage->pDat[i] = Input;
		}
		pAverage->Sum = Input * pAverage->Length;
		return Input;
	}
	
	pAverage->Sum -= pAverage->pDat[pAverage->DatPos];
	pAverage->pDat[pAverage->DatPos] = Input;
	pAverage->Sum += pAverage->pDat[pAverage->DatPos];
	
	pAverage->DatPos++;
	if(pAverage->DatPos >= pAverage->Length)
	{
		pAverage->DatPos = 0;
	}
	
	return (pAverage->Sum / pAverage->Length);
}

/*
	描述：对数据进行RC滤波
	pResCop：RC滤波相关数据结构体指针，详细参考RESCOPPARAM
	Input：实际输入值
	返回：滤波后的输出值
	注意：此函数中的k，代表旧新数据比为k:(1000-k),使用时需要考虑数据超长（int32_t）,
		另需注意，输入值单步跳动较小时，会因为单片机的舍余运算，导致滤波结果和实际数据一直保存偏差
*/
int32_t Mod_Filter_ResCop(RESCOPPARAM *pResCop, int32_t Input)
{
	if(pResCop->K > 999)
	{
		return 0;
	}
	
	if(pResCop->OnceTF == 0)
	{
		pResCop->OnceTF = 1;
		pResCop->DatLog = Input;
		return Input;
	}
	
	pResCop->DatLog = (pResCop->DatLog * pResCop->K + Input * (1000 - pResCop->K)) / 1000;
	
	return pResCop->DatLog;
}

/*
	描述：对数据进行RC滤波，第二方式
	pResCop：RC滤波相关数据结构体指针，详细参考RESCOPPARAM
	Input：实际输入值
	返回：滤波后的输出值
	注意：此函数中的k，代表旧新数据比为k:1，最大倍率为100,使用时需要考虑数据超长（int32_t）,
		另需注意，输入值单步跳动较小时，会因为单片机的舍余运算，导致滤波结果和实际数据一直保存偏差
*/
int32_t Mod_Filter_ResCop_V2(RESCOPPARAM *pResCop, int32_t Input)
{
	if(pResCop->K > 100)
	{
		return 0;
	}
	
	if(pResCop->OnceTF == 0)
	{
		pResCop->OnceTF = 1;
		pResCop->DatLog = Input;
		return Input;
	}
	
	pResCop->DatLog = (pResCop->DatLog * pResCop->K + Input) / (pResCop->K + 1);
	
	return pResCop->DatLog;
}

/*
	描述：对数据进行卡尔曼滤波
	kfp：卡尔曼滤波相关数据结构体指针，详细参考KALMANPARAM
	Input：实际输入值
	返回：滤波后的输出值
	注意：此函数采用浮点变量，使用时要考虑运算成本。
*/
float Mod_Filter_Kalman(KALMANPARAM *kfp,float input)
{
	//预测协方差方程：k时刻系统估算协方差 = k-1时刻的系统协方差 + 过程噪声协方差
	kfp->Now_P = kfp->Last_P + kfp->Q;
	
	//卡尔曼增益方程：卡尔曼增益 = k时刻系统估算协方差 / （k时刻系统估算协方差 + 观测噪声协方差）
	kfp->Kg = kfp->Now_P / (kfp->Now_P + kfp->R);
	
	//更新最优值方程：k时刻状态变量的最优值 = 状态变量的预测值 + 卡尔曼增益 * （测量值 - 状态变量的预测值）
	kfp->out = kfp->out + kfp->Kg * (input - kfp->out);//因为这一次的预测值就是上一次的输出值
	
	//更新协方差方程: 本次的系统协方差付给 kfp->LastP 威下一次运算准备。
	kfp->Last_P = (1-kfp->Kg) * kfp->Now_P;
	
	return kfp->out;
}

/*
	描述：延迟一个数据周期，对数据进行剔除处理
	pScreen：剔除功能相关数据结构体指针，详细参考SCREENPARAM
	Input：实际输入值
	返回：若数据正常，返回第二个数据，若数据不正常，返回第三个数据
*/
int32_t Mod_Filter_Screen(SCREENPARAM *pScreen, int32_t Input)
{
	if(pScreen->OnceTF == 0)
	{
		pScreen->OnceTF = 1;
		pScreen->Dat[2] = Input;
		pScreen->Dat[1] = Input;
		pScreen->Dat[0] = Input;
		return Input;
	}
	
	pScreen->Dat[2] = pScreen->Dat[1];
	pScreen->Dat[1] = pScreen->Dat[0];
	pScreen->Dat[0] = Input;
	
	if((pScreen->Dat[1] > pScreen->Dat[0]) && (pScreen->Dat[1] > pScreen->Dat[2]))
	{
		if(((pScreen->Dat[1] - pScreen->Dat[0]) > pScreen->Limit) && ((pScreen->Dat[1] - pScreen->Dat[2]) > pScreen->Limit))
		{
			pScreen->Dat[1] = pScreen->Dat[2];
		}
	}
	if((pScreen->Dat[0] > pScreen->Dat[1]) && (pScreen->Dat[2] > pScreen->Dat[1]))
	{
		if(((pScreen->Dat[0] - pScreen->Dat[1]) > pScreen->Limit) && ((pScreen->Dat[2] - pScreen->Dat[1]) > pScreen->Limit))
		{
			pScreen->Dat[1] = pScreen->Dat[2];
		}
	}
	return pScreen->Dat[1];
}

mod_filter.h源码

#ifndef __MOD_FILTER_H__
#define __MOD_FILTER_H__


typedef struct AVERAGEPARAMSTRUCT
{
	int32_t *pDat;  //数据指针，需要另行定义数组
	uint8_t DatPos;  //数据位置
	int32_t Sum;  //所有数据的和
	uint8_t Length;  //数据均值长度
	uint8_t OnceTF;  //初次运行标志
}AVERAGEPARAM;

typedef struct RESCOPPARAMSTRUCT
{
	int32_t DatLog;  //上一次的计算值
	uint16_t K;  //比例系数1~1000;
	uint8_t OnceTF;  //初次运行标志
}RESCOPPARAM;

typedef struct KALMANPARAMSTRUCT
{
	float Last_P;  //上次估算协方差
	float Now_P;  //当前估算协方差
	float out;  //卡尔曼滤波器输出
	float Kg;  //卡尔曼增益
	float Q;  //过程噪声协方差
	float R;  //观测噪声协方差
}KALMANPARAM;

typedef struct SCREENPARAMSTRUCT
{
	int32_t Dat[3];  //数据
	uint8_t OnceTF;  //初次运行标志
	uint32_t Limit;  //剔除标准
}SCREENPARAM;

extern int32_t Mod_Filter_Average(AVERAGEPARAM *pAverage, int32_t Input);
extern int32_t Mod_Filter_ResCop(RESCOPPARAM *pResCop, int32_t Input);
extern int32_t Mod_Filter_ResCop_V2(RESCOPPARAM *pResCop, int32_t Input);
extern float Mod_Filter_Kalman(KALMANPARAM *kfp,float input);
extern int32_t Mod_Filter_Screen(SCREENPARAM *pScreen, int32_t Input);

#endif

二、总述

1、涉及到数据采集的地方，就一定会遇到干扰，遇到干扰，就会用到滤波。滤波就是把有用的信息通过，把无用的信息阻断。滤波有多种方式，每种方式都有自己的优势和劣势，每种算法也都有自己的缺陷。

2、此模块是把均值滤波，RC滤波，卡尔曼滤波（简易版），数据剔除滤波做成函数，集中放置在一起。使用的时候，需要定义对应的结构体变量并初始化，然后调用函数处理。

3、借此，博主根据自己的使用经验，大胆的分析一下各种滤波方式的差别，有不对的地方，希望能不吝赐教。

三、均值滤波（平滑滤波）

3.1、滤波原理

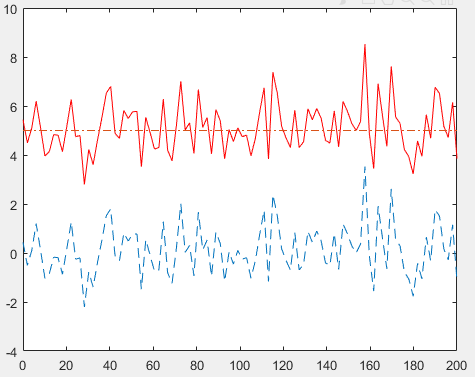
1、首先假设一种理想状态，现在有一个电压信号是两个信号的叠加（记作合成信号‘实线’），源信号是一个稳定的电压5V（‘-.-.-’），噪声是均值为0、标准差为1的正态分布的波动电压(‘—–‘)。波形图如下。

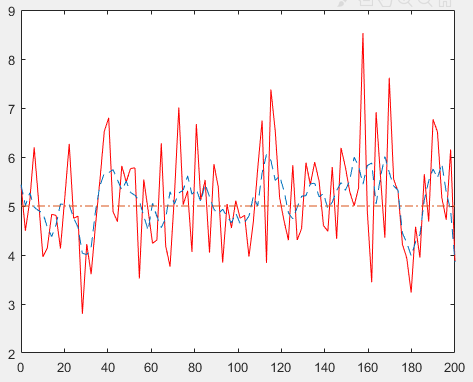
2、从波形图就能直观的看出来，合成信号实际是在源信号附近波动。如果把合成信号高出5V的部分和低出5V的部分相互抵消，就能得到一个类似源信号的波形。实际情况也是这样，由于正态分布的特性，噪声在0V左右的分布是”对称“的。对应的，合成信号在源信号附近的波动整体成”对称“的。只需要将多个采样之间进行相加求平均值，就能得到和源信号相近的结果。

3、处理后的数据确实出现了收敛，但上图的滤波效果显然不是很理想，既然均值滤波是多个数据之间求取平均值，那均值处理的数据越多，单个数据对整体的影响就小，那么滤波强度就会越强。

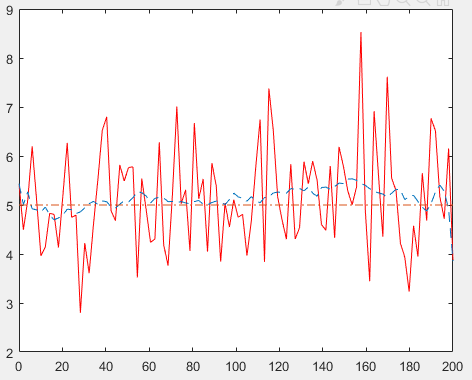
4、二十次采样做均值效果果然更加明显。但是采样是连续线性采样，而求取平均值需要将多次采样融合处理，这样就导致了数据延后。也就是计算出的结果并非当前值，而是从当前向后一段时间的整体值。如果源信号比较平稳那还好，如果源信号是波动的，势必会造成数据延后。

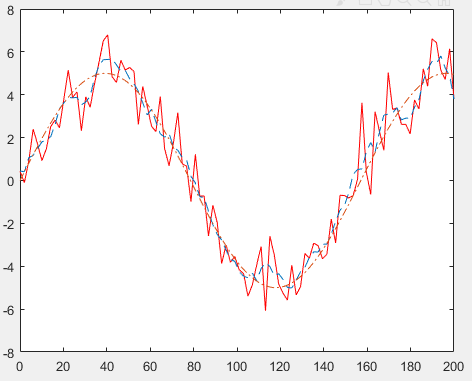
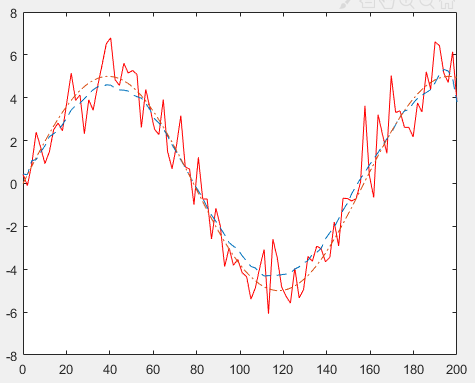
5、如上两图，五次采样做均值处理的时候，滤波效果较差，但是基本符合源信号。二十次采样做均值处理的时候，就和源信号相差较远了。

6、前面我们假设噪声是正态分布，实际使用中，噪声肯定不会这么配合我们。但是大多数情况下，噪声都大致对称，均值滤波的适用范围还是比较广的。

3.2、用法介绍

//首先需要定义一个结构体变量
AVERAGEPARAM AverAge_Demo;

//然后需要定义存放历史数据的数组，根据均值长度定义
int32_t Dat_Demo[20];

//对数据进行初始化
void Demo_Init(void)
{
	uint8_t i;

	AverAge_Demo.pDat = Dat_Demo;  //数据指针
	AverAge_Demo.DatPos = 0;  //数据位置
	AverAge_Demo.Sum = 0;  //所有数据的和
	AverAge_Demo.Length = 20;  //数据均值长度
	AverAge_Demo.OnceTF = 0;  //初次运行标志

	for(i=0; i<AverAge_Demo.Length; i++)
	{
		AverAge_Demo.pDat[i] = 0;
	}
}

//实际执行
OutDat = Mod_Filter_Average(&AverAge_Demo, InDat);

3.3、注意事项

1、要评估被滤波数据的大小，进而确定均值滤波的长度。AverAge_Demo.pDat指向的数据之和，不能超出int32_t类型的总和。

2、均值滤波要综合滤波效果和失真，均值处理的数据太少，滤波效果不明显，处理的数据太多，会导致数据失真。

3、博主曾经遇到过一种情况，IO读取PWM的占空比的时候，总是在平稳状态下突然来一次异常。均值滤波总是要等待这次异常逐步移动到数组的末尾，才能完全消除异常的影响。所以说，均值滤波对于非正态分布的噪声处理是很不友好的。

四、RC滤波（一阶低通滤波）

4.1、滤波原理

1、软件RC滤波的来源是硬件，那就先分析硬件上的RC滤波原理，具体的叫法，应该是一阶RC低通滤波器。

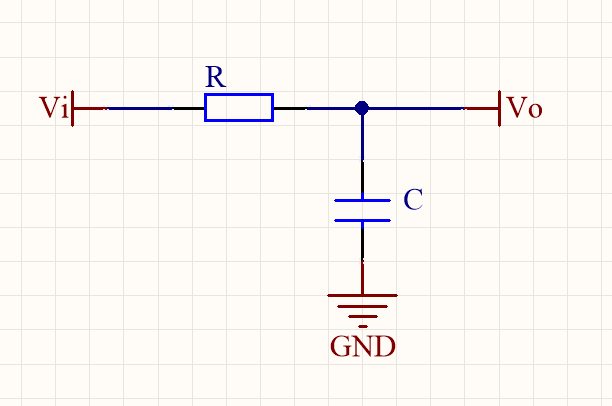
2、上图中，Vi是输入信号，经过电阻电容组成的滤波器后，输出信号Vo。先简单的从原理上进行分析，电容有一个特点就是通高频，阻低频。所以信号经过滤波器的时候，高频信号被导向地，低频信号则能被Vo检测到。

3、从公式也能分析出来。首先电容的容抗公式是\(\frac{1}{j{\omega}C}\)，j表示复数的虚部，ω表示角频率，C是电容的容值。已知电阻R，输入电压Vi，通过电阻分压，可以计算得到\[Vo=Vi\times\frac{1}{1+j{\omega}RC}\]

上式再经过转换，得到输出和输入之比，即信号增益相关公式\[H(j{\omega})=\frac{Vo}{Vi}=\frac{1}{1+j{\omega}RC}\]

再进行转换并求模，具体转换过程可以参考https://blog.csdn.net/zwc475793240/article/details/122432824
大致是分子分母同时乘一复数，将分母从复数转换为实数，再用勾股定理进行求模。\[|H(j{\omega})|=\sqrt{\frac{1}{1+({\omega}RC)^2}}\]

从公式即可看出，当角频率ω增大时，增益减弱，当角频率ω减小时，增益加强。并且从公式可以看出，信号只要讲过RC滤波器必定会有衰减，只是程度的问题。信号只要经过滤波器，也不可能完全消除掉。
一般当增益达到\(\frac{\sqrt{2}}{2}\)以下时，视为截止，又有\({\omega}=2{\pi}f\)由此可得RC滤波截止频率计算公式为\[f=\frac{1}{2{\pi}RC}\]

4、通过上述分析，我们已经知道了RC滤波器的原理和截止频率的计算公式。但是上述全部是在频域进行分析，如果想要应用到程序中，必须要有时域公式，才能列出程序算法。

首先假设电阻R分压为Vr，则有\(Vo=Vi-Vr\)，假设Vo端是高阻态，则流经电阻和电容的电流相同，设为Ir。流经电容的电流又可以通过电荷和时间关系获得，即\(Ir=\frac{dq}{dt}\)。又因电容的电荷\(Q=UC\)。所以，\(Ir=C\frac{dVo}{dt}\)由此得到微分方程\[Vo=Vi-RC\frac{dVo}{dt}\]

将上式进行离散，即可得到公式\[Vo(k)=\frac{Vi(k)+\frac{RC}{{\Delta}t}Vo(k-1)}{1+\frac{RC}{{\Delta}t}}\]

RC是通过截止频率计算得到的常量，Δt对应我们程序采样的周期，因此\(\frac{RC}{{\Delta}t}\)是一个常量，上式可以解释为，通过将本次采样值和上次计算值进行计算，得到本次的计算值。

当然，如果消除掉Vi(k)和Vo(k-1)的影响，就能很清晰的看到，RC滤波就是从上次的输出值和本次采样值之间取不同信任度，而输出一个新的输出值。

4.2、用法介绍

//首先需要定义一个结构体变量
RESCOPPARAM ResCop_Demo;

//对数据进行初始化
void Demo_Init(void)
{
	ResCop_Demo.DatLog = 0;  //上一次的计算值
	ResCop_Demo.K = 10;  //比例系数1~1000,即RC/Δt;
	ResCop_Demo.OnceTF = 0;  //初次运行标志
}

//实际执行
OutDat = Mod_Filter_ResCop_V2(&ResCop_Demo, InDat);

//或者使用变格式的函数，具体可以参考源代码，此时的K已经不代表RC/Δt了
OutDat = Mod_Filter_ResCop(&ResCop_Demo, InDat);

4.3、注意事项

1、从公式上已经分析到，所有信号经过一阶RC低通滤波器之后，信号都会出现衰减，实际使用中应该考虑到这些。其次RC滤波有比较明显的延后性，可参考如下波形图。

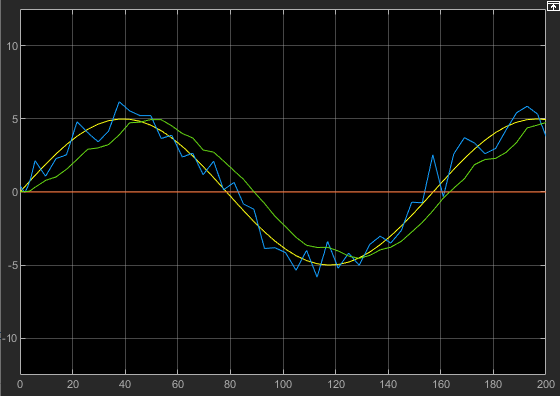
2、考虑到单片机普遍运算能力吃紧，所以此函数没有采用浮点运算。使用的过程中要考虑到信号数值大小和K值的关系，K值太大，由于单片机的舍余运算，会导致计算值一直无法达到实际值。此时可以将采集到的数据进行放大，计算之后再进行缩小。

持续更新中。。。

一	二	三	四	五	六	日
		1	2	3	4	5
6	7	8	9	10	11	12
13	14	15	16	17	18	19
20	21	22	23	24	25	26
27	28	29	30	31